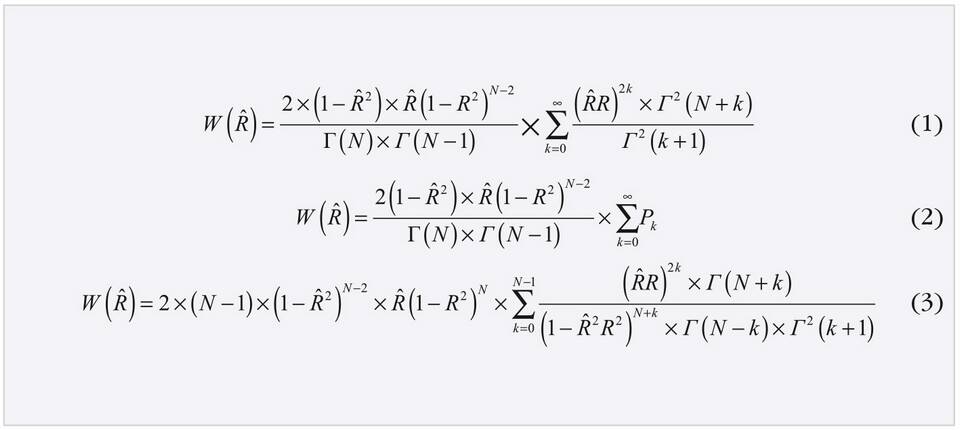Бесконечный ряд - это сумма бесконечного количества слагаемых. Для нахождения его суммы необходимо определить сходимость ряда и применить соответствующие методы вычисления.
Содержание
Основные понятия бесконечных рядов
Бесконечный ряд - это сумма бесконечного количества слагаемых. Для нахождения его суммы необходимо определить сходимость ряда и применить соответствующие методы вычисления.
Типы бесконечных рядов
| Тип ряда | Пример | Условие сходимости |
| Геометрический | 1 + 1/2 + 1/4 + 1/8 + ... | |r| < 1 |
| Гармонический | 1 + 1/2 + 1/3 + 1/4 + ... | Расходится |
| Знакопеременный | 1 - 1/2 + 1/3 - 1/4 + ... | Сходится условно |
Методы нахождения суммы
Геометрический ряд
Формула суммы: S = a₁ / (1 - r), где |r| < 1
- Определите первый член (a₁) и знаменатель (r)
- Проверьте условие сходимости |r| < 1
- Примените формулу суммы
Телескопический ряд
- Представьте общий член в виде разности
- Запишите частичную сумму
- Найдите предел при n → ∞
Примеры вычислений
| Ряд | Решение | Сумма |
| 1 + 1/2 + 1/4 + 1/8 + ... | S = 1/(1 - 1/2) | 2 |
| 1/2 + 1/6 + 1/12 + 1/20 + ... | 1/(n(n+1)) = 1/n - 1/(n+1) | 1 |
Критерии сходимости
- Признак Даламбера
- Признак Коши
- Интегральный признак
- Признак Лейбница для знакопеременных рядов
Специальные случаи
Ряд Тейлора
- Разложите функцию в ряд
- Определите область сходимости
- Вычислите сумму при заданных значениях
Дзета-функция Римана
- ζ(s) = Σ 1/nˢ
- Сходится при s > 1
- ζ(2) = π²/6
Практические рекомендации
- Всегда проверяйте сходимость ряда перед вычислением суммы
- Используйте разложение на простые дроби для сложных рядов
- Применяйте методы интегрирования для оценки суммы
- Проверяйте результаты с помощью численных методов
Заключение
Вычисление суммы бесконечного ряда требует понимания его природы и свойств. Для разных типов рядов применяются различные методы: от простой формулы геометрической прогрессии до сложных аналитических приемов. Правильное определение сходимости ряда - ключевой этап перед нахождением его суммы.
